\[\newcommand{\KO}{\mathrm{KO}} \newcommand{\TMF}{\mathrm{TMF}} \newcommand{\KU}{\mathrm{KU}} \newcommand{\Mfg}{M_\mathrm{fg}} \newcommand{\spec}{\mathrm{Spec}} \newcommand{\dX}{\mathcal{X}} \newcommand{\co}{\mathcal{O}} \newcommand{\Z}{\mathbf{Z}} \newcommand{\top}{\mathrm{top}} \newcommand{\E}{\mathbf{E}} \newcommand{\GG}{\mathbf{G}} \newcommand{\DD}{\mathbf{D}} \newcommand{\Mell}{M_\mathrm{ell}} \newcommand{\ce}{\mathcal{E}} \newcommand{\H}{\mathrm{H}} \newcommand{\dR}{\mathrm{dR}} \newcommand{\cf}{\mathcal{F}} \newcommand{\FF}{\mathbf{F}} \newcommand{\spf}{\mathrm{Spf}\ } \newcommand{\cA}{\mathcal{A}} \newcommand{\Mcub}{M_\mathrm{cub}} \newcommand{\Mqd}{M_\mathrm{qd}} \newcommand{\Aut}{\mathrm{Aut}} \newcommand{\tmf}{\mathrm{tmf}} \newcommand{\Tmf}{\mathrm{Tmf}} \newcommand{\Map}{\mathrm{Map}} \newcommand{\Ext}{\mathrm{Ext}} \newcommand{\End}{\mathrm{End}} \newcommand{\cg}{\mathcal{G}} \newcommand{\Hom}{\mathrm{Hom}} \newcommand{BP}[1]{\mathrm{BP}\langle #1\rangle} \newcommand{\QQ}{\mathbf{Q}} \newcommand{\PP}{\mathbf{P}} \newcommand{\Gal}{\mathrm{Gal}} \newcommand{\proj}{\mathrm{Proj}\ } \newcommand{\Ltwo}{L_{K(2)}} \newcommand{\Eoo}{\mathbf{E}_\infty} \newcommand{\ol}[1]{\overline #1} \newcommand{\pic}{\mathrm{Pic}} \newcommand{\RP}{\mathbf{R}P} \newcommand{\BO}{\mathrm{BO}} \newcommand{\cc}{\mathbf{C}} \newcommand{\CP}{\mathbf{CP}} \newcommand{\wt}[1]{\widetilde #1} \newcommand{\RR}{\mathbf{R}} \renewcommand{\S}{\mathbb{S}} \newcommand{\Lone}{L_{K(1)}} \newcommand{\Ltwo}{L_{K(2)}} \newcommand{\gl}{\mathrm{gl}} \newcommand{\Lk}{L_{K(n)}} \newcommand{\ku}{\mathrm{ku}} \newcommand{\ko}{\mathrm{ko}} \newcommand{\GL}{\mathrm{GL}} \newcommand{\Ln}{L_n} \newcommand{\Lt}{L_{K(t)}} \newcommand{\W}{\mathrm{W}} \newcommand{\BU}{\mathrm{BU}} \newcommand{\SU}{\mathrm{SU}} \newcommand{\MU}{\mathrm{MU}} \newcommand{\ul}[1]{\underline #1} \newcommand{\Sq}{\mathrm{Sq}} \newcommand{\Tr}{\mathrm{Tr}} \newcommand{\d}{\mathrm{d}} \newcommand{\HP}{\mathrm{HP}} \newcommand{\cL}{\mathcal{L}} \newcommand{\cs}{\mathrm{cs}} \newcommand{\cd}{\mathcal{D}} \newcommand{\Bord}{\mathrm{Bord}} \newcommand{\SO}{\mathrm{SO}} \newcommand{\cC}{\mathcal{C}} \newcommand{\Sp}{\mathrm{Sp}} \newcommand{\Lkd}{L_{K(d)}} \newcommand{\Mod}{\mathrm{Mod}} \newcommand{\cH}{\mathcal{H}} \newcommand{\ket}[1]{|#1 \rangle} \newcommand{\Bun}{\mathrm{Bun}} \newcommand{\cM}{\mathcal{M}} \newcommand{\MTH}{\mathrm{MT}H} \newcommand{\MSO}{\mathrm{MSO}} \newcommand{\twsm}{\ \widetilde{\wedge} \ } \newcommand{\BSpin}{\mathrm{BSpin}} \newcommand{\MSpin}{\mathrm{MSpin}} \newcommand{\BString}{\mathrm{BString}} \newcommand{\MString}{\mathrm{MString}} \newcommand{\B}{\mathrm{B}} \newcommand{\der}{\mathrm{der}} \newcommand{\Cat}{\mathrm{Cat}} \newcommand{\QCoh}{\mathrm{QCoh}} \newcommand{\LMod}{\mathrm{LMod}} \newcommand{\Rep}{\mathrm{Rep}} \newcommand{\HH}{\mathrm{HH}} \newcommand{\ZZ}{\mathfrak{Z}} \newcommand{\fr}{\mathrm{fr}} \newcommand{\BSO}{\mathrm{BSO}} \newcommand{\BSU}{\mathrm{BSU}} \newcommand{\id}{\mathrm{id}} \newcommand{\Top}{\mathrm{Top}} \newcommand{\cP}{\mathcal{P}} \newcommand{\U}{\mathrm{U}} \newcommand{\Sym}{\mathrm{Sym}} \newcommand{\coker}{\mathrm{coker}} \newcommand{\Vect}{\mathrm{Vect}} \newcommand{\Fun}{\mathrm{Fun}} \newcommand{\cT}{\mathcal{T}} \newcommand{\cJ}{\mathcal{J}} \newcommand{\Res}{\mathrm{Res}} \newcommand{\Ind}{\mathrm{Ind}} \newcommand{\MO}{\mathrm{MO}} \newcommand{\MSO}{\mathrm{MSO}} \newcommand{\colim}{\mathrm{colim}} \newcommand{\hocolim}{\mathrm{hocolim}} \newcommand{\fin}{\mathrm{fin}} \newcommand{\Tot}{\mathrm{Tot}} \newcommand{\im}{\mathrm{im}} \newcommand{\FT}{\mathrm{FT}} \newcommand{\AA}{\mathbf{A}} \newcommand{\Frob}{\mathrm{Frob}} \newcommand{\ex}{\mathrm{ex,pr}} \newcommand{\fil}{\mathrm{fil}} \newcommand{\gr}{\mathrm{gr}} \newcommand{\un}{\mathrm{un}} \newcommand{\Syn}{\mathrm{Syn}} \newcommand{\Cart}{\mathrm{Cart}} \newcommand{\bo}{\mathrm{bo}} \newcommand{\mmod}{/\!\!/} \newcommand{\bsp}{\mathrm{bsp}} \newcommand{\BPP}{\mathrm{BP}} \newcommand{\CAlg}{\mathrm{CAlg}} \newcommand{\TCart}{\mathrm{TCart}} \newcommand{\BW}{\mathrm{BW}} \newcommand{\Br}{\mathrm{Br}} \newcommand{\Pic}{\mathrm{Pic}} \newcommand{\ext}{\mathrm{ext}} \newcommand{\Cl}{\mathrm{Cl}} \newcommand{\disc}{\mathrm{disc}} \newcommand{\dir}{D\!\!\!\!/} \newcommand{\bb}{\mathrm{bb}} \newcommand{\Ran}{\mathrm{Ran}} \newcommand{\cu}{\mathcal{U}} \newcommand{\Gr}{\mathrm{Gr}} \newcommand{\Alg}{\mathrm{Alg}} \newcommand{\G}{\Gamma} \newcommand{\dY}{\mathcal{Y}} \newcommand{\Line}{\mathrm{Line}} \newcommand{\MUP}{\mathrm{MUP}} \newcommand{\Bl}{\mathrm{Bl}} \newcommand{\St}{\mathrm{St}} \newcommand{\cB}{\mathcal{B}} \newcommand{\SL}{\mathrm{SL}} \newcommand{\XX}{\mathrm{X}} \newcommand{\gp}{\mathrm{gp}} \newcommand{\Q}{\mathrm{Q}} \newcommand{\cI}{\mathcal{I}} \newcommand{\T}{\mathrm{T}} \newcommand{\D}{\mathrm{D}} \newcommand{\Aff}{\mathrm{Aff}} \newcommand{\BGL}{\mathrm{BGL}} \newcommand{\an}{\mathrm{an}} \newcommand{\Tel}{\mathrm{Tel}} \renewcommand{\|}{|} \newcommand{\MGL}{\mathrm{MGL}} \newcommand{\CH}{\mathrm{CH}} \newcommand{\fr}[1]{\mathfrak #1} \newcommand{\ch}{\mathrm{ch}} \newcommand{\Td}{\mathrm{Td}} \newcommand{\Spin}{\mathrm{Spin}} \newcommand{\G}{\mathrm{G}} \newcommand{\cHH}{\mathcal{H}} \newcommand{\F}{\mathrm{F}} \newcommand{\B}{\mathrm{B}} \newcommand{\HC}{\mathrm{HC}} \newcommand{\fib}{\mathrm{fib}} \newcommand{\tr}{\mathrm{tr}} \newcommand{\TR}{\mathrm{TR}} \newcommand{\THH}{\mathrm{THH}} \newcommand{\TP}{\mathrm{TP}} \newcommand{\crys}{\mathrm{crys}} \newcommand{\even}{\mathrm{even}} \newcommand{\odd}{\mathrm{odd}} \newcommand{\hodge}{\mathrm{Hodge}} \newcommand{\V}{\mathrm{V}} \newcommand{\C}{C} \newcommand{\K}{K} \newcommand{\M}{M} \newcommand{\X}{X} \newcommand{\h}{h} \newcommand{\TC}{\mathrm{TC}} \newcommand{\t}{t} \newcommand{\DC}{\mathrm{DC}} \newcommand{\str}{\mathrm{str}} \newcommand{\gen}{\mathrm{gen}} \newcommand{\Cyc}{\mathrm{CycSp}} \newcommand{\DA}{\mathrm{DA}} \newcommand{\AG}{\mathbf{A}^1/\mathbf{G}_m} \newcommand{\Crys}{\mathrm{Crys}} \newcommand{\cV}{\mathcal{V}} \newcommand{\can}{\mathrm{can}} \newcommand{\Coh}{\mathrm{Coh}} \newcommand{\SH}{\mathrm{SH}} \newcommand{\cbr}[1]{\left\{ #1 \right\}} \newcommand{\prn}[1]{\left( #1 \right)} \newcommand{\vol}{\operatorname{vol}} \newcommand{\id}{\operatorname{id}} \newcommand{\STan}{\mathbf{sTAN}} \newcommand{\bm}{\mathbf{m}} \newcommand{\bE}{\mathbf{E}} \newcommand{\bS}{\mathbf{S}} \newcommand{\cT}{\mathcal{T}} \newcommand{\NN}{\mathbb{N}}\]

Since the last post I made, I realized a small (big) mistake that I had made; it’s harder than expected to define an \(\ell\)-fold category structure on the \(\ell\) pieces. I’ll try to rework this in a restricted case.

See part 1 here and see part 2 here.

(Last updated Nov. 13, 2020)

What an idempotent \(\ell\) piece is

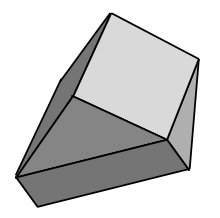
Recall the decomposition of tangles in \(S^3\) into a cycle of tangles, and then a decomposition of one of those tangles into a cycle. The resulting objects are tangles in gyrobifastigia; the ambient piece containing the tangle is pictured as follows.

There’s a central property relating to this ambient 2-piece \((P,\prn{\cbr{V_i}})\); we have \(V_{2i} = V_{2i+1}\), and we have the composition

$$(P,\prn{\cbr{V_i}}) \circ_{\id_j} (P,\prn{\cbr{V_i}}) = (P,\prn{\cbr{V_i}})$$

defined via the identity map \(V_{2j+1} \rightarrow V_{2j}\). This yields closure under composition of tangles in the 2-piece. We give this as a general definition now:

Definition. We say that an \(\ell\)-piece \(\prn{P,\prn{\cbr{V_i}}}\) is idempotent if \(V_{2i} = V_{2i+1}\) and, for all identity maps \(\id_j:V_{2j + 1} \rightarrow V_{2i}\) we have

$$(P,\prn{\cbr{V_i}}) \circ_{\id_j} (P,\prn{\cbr{V_i}}) = (P,\prn{\cbr{V_i}})$$

We can talk about tangles in idempotent \(\ell\)-pieces; these yield a similar story to the square tangles before, because the class of tangles in an idempotent \(\ell\)-piece is closed under composition. This time, composition is canonical given an isotopy class of \(\ell\)-tuples of 0-submanifolds of \(\cbr{V_i}\). We’ll develop this now, but first we give a relevant notion of hyperbolicity.

Asymptotic hyperbolicity of pieces

Definition. An \(\ell\)-piece \((P,\prn{\cbr{V_i}})\) is called asymptotically \(\ell\)-hyperbolic if there exists some \(\bm \in 2\NN^\ell\) such that \((P,\prn{\cbr{V_i}})\) is \(\bm'\)-hyperbolic for all \(\bm' \geq \bm\) in the product order.

Recall that a composition of \(n\)-many \((2nm_1,2m_2,\dots,2m_\ell)\)-hyperbolic \(\ell\)-pieces is \((2m_1,2m_2,\dots,2m_\ell)\)-hyperbolic. Hence the class of asymptotically \(\ell\)-hyperbolic 3-manifolds is closed under composition. This is powerful enough to be an obstacle.

Proposition. Suppose \((P,\prn{\cbr{V_i}})\) is an idempotent \(\ell\)-piece which is \(\bm\)-hyperbolic for some \(\bm \in 2\NN^\ell\). Then, it is \(\prn{2,\dots,2}\)-hyperbolic, and we have

$$\vol^{\bm}(P,\prn{\cbr{V_i}}) = \frac{\vol^{(2,\dots,2)}(P,\prn{\cbr{V_i}})}{\prod_i m_i}$$

In fact, by idempotence, we have \(D^{\bm'}(P,\prn{\cbr{V_i}}) = D^{\bm}(P,\prn{\cbr{V_i}})\) for any \(\bm,\bm' \in 2\NN^\ell\). Hyperbolicity is hence equivalent regardless of the index, and the inequality follows immediately.

This feels overpowered to the point of probable contradiction; by doubling across all indices other than 1, if we can prove that there are no \(2\)-hyperbolic idempotent pieces, then we can prove that there are no \(\bm\)-hyperbolic idempotent \(\ell\)-pieces. For this, it would be sufficient to prove that there exists some constant \(\varepsilon > 0\) such that the \(2m\)-hyperbolic volume of all pieces is at least \(\varepsilon > 0\); unfortunately the Naive bound depends on \(\frac{1}{2m}\), so we don’t have this result.

Some time in the future, it would be interesting to search for either idempotent 2-hyperbolic pieces or to search for a proof that no such pieces exist. The most obvious examples–idempotent tangles in a wedge of \(S^3\) or in a gyrobifastigium–all seem to fail. We’ll bin this question for now, and instead talk about general tangles living in an idempotent tangle.

(Hyperbolic) tangles in an idempotent piece

As noted above, the class of tangles in a particular idempotent piece is closed under composition, and composition is canonical given an isotopy class of \(\ell\)-tuples of 0-submanifolds of \(\cbr{V_i}\). Given a particular idempotent \(\ell\)-piece \((P,\prn{\cbr{V_1}})\) we’ll build up the structure of an \(\ell\)-fold category on the tangles in \((P,\prn{\cbr{V_i}})\), henceforth referred to as tangles in \(P\). This will be developed with a single trivial \((\ell-2)\)-cell, with a collection of \((\ell-1)\)-fold categories making up the \((\ell-1)\)-cells and a suitable collection of crossed objects which will make up the \(\ell\)-cells.

Definition. We define the \((\ell-1)\)-fold category \(\cC_i\) with a single trivial \((\ell-2)\)-cell and \((\ell-1)\)-cells given by the isotopy classes of 0-submanifolds of \(V_i\). Since \((P,\prn{\cbr{V_i}})\) is idempotent, we may define the composition of submanifolds \(M \circ_{2j} M'\) for \(j \neq i\) by the 0-submanifold of \(V_i\) defined under the composition along the \(2j\)-indexed pair of faces.

I’ll handwave this away, but this is a genuine \((\ell-1)\)-fold category, as it satisfies the evident interchange law implies by the interchange law for composition of \(\ell\)-pieces. I’d rather give a bit of characterization on \(\cC_i\), delivered via the following construction that I’m making up.

For every monoid \(M_i\), there is an \(\ell\)-fold category \(M_i\) with a trivial \((\ell-1)\)-cell and a collection of \(\ell\)-cells such that all compositions are defined by the monoid action. That is, every one of the \(\ell\) categories of \(\ell\)-cells is the delooping which realizes \(M_i\) as a one-object category.

This allows for the following proposition:

Proposition. Suppose that \(V_i\) has \(n\) connected components. Then, the \((\ell-1)\)-fold category \(\cC_i\) is given by \(\NN^n\).

Proof sketch. An element of \(\cC_i\) is an isotopy class of 0-submanifolds of \(M_i\); these are equivalent to a disjoint union of isotopy classes of connected 0-submanifolds, which itself is given by a choice of connected component. Hence there is a bijection between \(\cC_i\) and \(\NN^n\) given by counting the points per component. We show that this is functorial for each type of composition.

\(V_i\) is glued to itself in composition \(V_i \circ_j V_i\) via two diffeomorphic properly embedded 1-manifolds \(T_2\) in the first copy and \(T_1\) in the second. Each connected component of \(V_i\) must intersect \(T_1\); idempotence and a little bit of cleverness yields that there are \(n\) connected components of \(T_1\), each intersecting exactly one of the components of \(V_i\). The same is true for \(T_2\), and the two “sides” of a glued component of \(T_2\) and \(T_1\) correspond with copies of the same component in \(V_i\). This yields additivity.

This is nice, but not necessary for the following definition.

Definition. The \(\ell\)-fold category of tangles in \(P\) has \(i\)th \((\ell-1)\)-fold faces given by \(\cC_i\) and \(\ell\)-cells given by the tangles in \((P,\cbr{V_i})\).

Say that a tangle in \((P,\cbr{V_i})\) is an identity if it is the identity in one of the associated categories of \(\ell\)-cells. Then, one can form the category of asymptotically hyperbolic tangles and identities in \(P\).

Our statement that \(\ell\)-pieces decomposing into hyperbolic \((\ell+1)\)-pieces are hyperbolic then compiles down to a categorical statement about the relationships between categories of pieces. I won’t go into it further, as it isn’t super useful.

Limitations and the moral of the story

The moral of the story here might be that this simply is not very useful. This forms a useful visualization tool in very limited cases of tangles in familiar idempotent pieces 9such as gyrobifastiga), but it isn’t quite novel there, and the generalization is painful.

In particular, the generalization comes as a collection of (intuitively, not just set-theoretically) small categories of \(\ell\)-pieces; it would simply be more satisfying if there was a big \(\ell\)-fold category of all of the \(\ell\)-pieces. Unfortunately, then we would have to tack more data onto our categories so that two \(\ell\)-fold pieces without gluing given by an \(\ell\)-fold piece are not considered composable.

It is what it is.